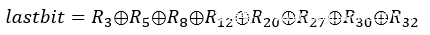BUU-crypto

[CISCN2018]oldstreamgame

参考文章:https://www.anquanke.com/post/id/181811#h2-0

flag = "flag{xxxxxxxxxxxxxxxx}"
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==14
#接收两个参数，R是32位的初始状态(即flag)，mask是32位的掩码，由于mask已知，所以我们就直接把他当做一个常数即可。
def lfsr(R,mask):
    output = (R << 1) & 0xffffffff  #把R左移一位后低32位,(即抹去R的最高位,然后在R的最低位补0)的值赋给output变量
    i=(R&mask)&0xffffffff#把传入的R和mask做按位与运算，运算结果取低32位，将该值赋给i变量。
    lastbit=0           #从i的最低位向i的最高位依次做异或运算，将运算结果赋给lastbit变量。
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
    output^=lastbit         #将output变量的最后一位设置成lastbit变量的值。
    return (output,lastbit) #返回output变量和lastbit变量的值，output即经过一轮lfsr之后的新序列，lastbit即经过一轮lfsr之后输出的一位。

R=int(flag[5:-1],16)
mask = 0b10100100000010000000100010010100

f=open("key","w")
for i in range(100):
    tmp=0
    for j in range(8):
        (R,out)=lfsr(R,mask)
        tmp=(tmp << 1)^out
    f.write(chr(tmp))
f.close()

1
2

# key

分析一下我们的已知条件：

1
2
3

已知初始状态的长度为4个十六进制数，即32位，初始状态的值即我们要去求的flag。
已知反馈函数，只不过这里的反馈函数是代码的形式，我们需要提取出它的数学表达式。
已知输出序列。

那么我们的任务很明确,就是通过分析lfsr函数,整理成数学表达式的形式求解即可,接下来我们对代码进行逐行解读

#接收两个参数，R是32位的初始状态(即flag)，mask是32位的掩码，由于mask已知，所以我们就直接把他当做一个常数即可。
def lfsr(R,mask):
#把R左移一位后低32位（即抹去R的最高位，然后在R的最低位补0）的值赋给output变量。
    output = (R << 1) & 0xffffffff
#把传入的R和mask做按位与运算，运算结果取低32位，将该值赋给i变量。
    i=(R&mask)&0xffffffff
#从i的最低位向i的最高位依次做异或运算，将运算结果赋给lastbit变量。
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
#将output变量的最后一位设置成lastbit变量的值。
    output^=lastbit
#返回output变量和lastbit变量的值，output即经过一轮lfsr之后的新序列，lastbit即经过一轮lfsr之后输出的一位。
    return (output,lastbit)

通过上面的分析，我们可以看出在这道题的情境下，lfsr函数本质上就是一个输入R输出lastbit的函数，虽然我们现在已经清楚了R是如何经过一系列运算得到lastbit的，但是我们前面的反馈函数都是数学表达式的形式，我们能否将上述过程整理成一个表达式的形式呢？这就需要我们再进一步进行分析：

mask = 0b10100100000010000000100010010100
mask只有第3、5、8、12、20、27、30、32这几位为1，其余位均为0。
mask与R做按位与运算得到i，当且仅当R的第3、5、8、12、20、27、30、32这几位中也出现1时，i中才可能出现1，否则i中将全为0。
lastbit是由i的最低位向i的最高位一次做异或运算得到的,在这个过程中，所有为0的位我们可以忽略不计(因为0异或任何数等于任何数本身,不影响最后运算结果),因此lastbit的值取决于i中有多少个1;当i中有奇数个1时，lastbit等于1;当i中有偶数个1时，lastbit等于0。

将其写成数学表示式的形式，即为：

显然，lastbit和R之间满足线性关系，那么接下来我们就可以开始求解了：

首先读取key

#python3 
import os,sys
os.chdir(sys.path[0])
from Crypto.Util.number import*
f = open('key','rb').read()
key = bytes_to_long(f)
bin_out = bin(key)[2:].zfill(100*8)
print(bin_out[:32]) #前32位就是key
#00100000111111011110111011111000

这里说的lastbit就是key的值

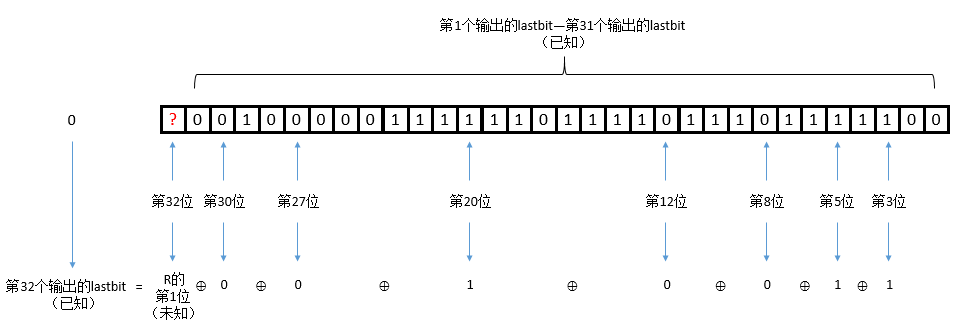
这样我们就可以求出R的第1位，同样的方法，我们可以求出R的第2位：

以此类推，R的全部32位我们都可以依次求出了，将这一计算过程写成代码形式如下：

mask = '10100100000010000000100010010100'
key =  '00100000111111011110111011111000'

tmp=key

R=''
for i in range(32):
    output = '?' + key[ : 31]
    ans = int(tmp[-1-i])^int(output[-3])^int(output[-5])^int(output[-8])^int(output[-12])^int(output[-20])^int(output[-27])^int(output[-30])
    
    R+=str(ans)
    key=str(ans)+key[:31]
R=format(int(R[::-1],2),'x')
flag="flag{"+R+"}"
print(flag)

int(R[::-1],2) 将二进制字符串 R 反转后，转换成对应的十进制整数。
format(..., 'x') 将第一步得到的十进制整数格式化为16进制字符串。其中，‘x’ 表示格式化为16进制，可以使用其他格式化选项，如 ‘o’ 表示8进制，‘b’ 表示2进制等。
最终的结果是将R从二进制格式转换为16进制字符串格式，并将其保存在R变量中。

Quoted-printable

=E9=82=A3=E4=BD=A0=E4=B9=9F=E5=BE=88=E6=A3=92=E5=93=A6

http://web.chacuo.net/charsetquotedprintable

这个解密还是不太熟悉,没看出来

丢失的MD5

import hashlib   
for i in range(32,127):
    for j in range(32,127):
        for k in range(32,127):
            m=hashlib.md5()
            m.update(('TASC'+chr(i)+'O3RJMV'+chr(j)+'WDJKX'+chr(k)+'ZM').encode())
            des=m.hexdigest()
            if 'e9032' in des and 'da' in des and '911513' in des:
                print (des)

如果不加.encode会报错

哈希函数需要的是字节（byte）类型的输入，而你传递了字符串类型。你可以通过将字符串编码为字节来解决这个问题。例如，将字符串编码为 UTF-8 格式的字节可以使用 .encode('utf-8') 方法。

大帝的密码武器

刚开始想的凯撒密码,但是理解错了它说的密文又想了轮转密码…结果卡住了

信息化时代的步伐

http://code.mcdvisa.com/

606046152623600817831216121621196386

凯撒？替换？呵呵!

这个确实不会

只解到这一步

1	FMAC{VNUVZQZNZQPKXQBIHRTHXRYBZQPKQVAMDAYVHAVYWNVZMQSHABQHXHPFXASH}

看WP都是用quipquip暴力破解

即

1	flag{substitutioncipherdecryptionisalwayseasyjustlikeapieceofcake}

whenthepigwanttoeat

传统知识+古典密码

先下载文件，发现有文件

第一个文件，信中的不同年份目前不知道是什么密码，应该属于传统知识了，然后对照表格，看各个年份分别对应的数字，发现分别是这几个数字： 28 30 23 08 17 10 16 30

然后再看到信的背面还有一个+甲子，一甲子=60年

然后把60加到上面一段数字中可以得到数字串：88 90 83 68 77 70 76 90

再然后把这些数字对应ASCII表，可以得到一串字母：XZSDMFLZ

然后把一串字母分别用栅栏和凯撒解密,先是栅栏密码，key=2，解密得到XMZFSLDZ，然后再用凯撒密码，key=5,解密得到SHUANGYU

这就是flag{SHUANGYU},附上解密工具网站：http://ctf.ssleye.com/?tdsourcetag=s_pcqq_aiomsg

至于为什么先是栅栏再是凯撒，是因为我先用凯撒解不出来。。。后来才换了栅栏。为什么key的值直接能给出2和5，因为借鉴的。。。
没做出来,感觉就是脑洞吧

脚本

栅栏密码解密：

def zhalan(e):
    elen = len(e)
    field = []
    for i in range(2, elen):
        if (elen % i == 0):
            field.append(i)

    for f in field:
        b = elen // f
        result = {x: '' for x in range(b)}
        for i in range(elen):
            a = i % b;
            result.update({a: result[a] + e[i]})
        d = ''
        for i in range(b):
            d = d + result[i]
        print(d)
        d.lower()


if __name__ == '__main__':
    e = 'XZSDMFLZ'
    zhalan(e)

然后就能解出两串字母，然后再用python脚本：

def casearDecrypt(ciphertext, source_char, destination_char, list_all):
    if list_all == True:
        for offset in range(1, 27):
            convertChar(offset)
    else:
        offset = ord(destination_char) - ord(source_char)
        convertChar(offset)


def convertChar(offset):
    chars = "abcdefghijklmnopqrstuvwxyz"
    for char in ciphertext:

        is_upper_flag = 0
        if char.isupper():
            char = char.lower()
            is_upper_flag = 1

        if char not in chars:
            outputChar(is_upper_flag, char)
            continue

        tempchar_ascii = ord(char) + offset
        tempchar = chr(tempchar_ascii)
        if tempchar not in chars:
            if offset < 0:
                tempchar_ascii += len(chars)
            else:
                tempchar_ascii -= len(chars)
        tempchar = chr(tempchar_ascii)
        outputChar(is_upper_flag, tempchar)
    print("")


def outputChar(is_upper_flag, char):
    if is_upper_flag == 1:
        print(char.upper(), end="")
    else:
        print(char, end="")


ciphertext = input("Please input ciphertext:\n")
while True:
    operation = input("List all results?y/n:")
    if operation == 'y' or operation == 'Y':
        casearDecrypt(ciphertext, '', '', True)
        break
    elif operation == 'n' or operation == 'N':
        des_char = input("Please input destination_char:\n")
        sors_char = input("Please input source_char:\n")
        casearDecrypt(ciphertext, sors_char, des_char, False)
        break
    else:
        print("Input error! Please input y/n:")

XMZFSLDZ
XSMLZDFZ

只能说这个脚本确实牛

RSA1

当 m<p或m<q时,直接脚本梭哈

import libnum
import gmpy2
from Crypto.Util.number import long_to_bytes,bytes_to_long

p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852

m = pow(c,dp,p)
m = pow(c,dq,q)
print(libnum.n2s(int(m)))

正常来说要利用中国剩余定理

1 2	m1=c^d mod p m2=c^d mod q

已知条件
c = m^e mod n
m = c^d mod n
ϕ(n)= (p−1)*(q−1)
d*e≡1 mod ϕ(n)
dp=d mod (p-1)
dq=d mod (q-1)

m=c^d mod n
m=c^d+k*n

'.' n=q*p
m=c^d+p*q*k

同时取余q和p

'.' m1=c^d mod q 所以
式1 c^d=kp+m1

式2 m2=c^d mod p

式1带入式2
m2=(kp+m1) mod q

等式两边同时减去m1
(m2-m1)*p≡kp mod q

因为gcd(p,q)=1
所以可以求p的逆元,得到
(m2-m1)*p-1≡k mod q

得到如下两个式子
k≡(m2-m1)*p-1 mod q

c^d=kp+m1
m≡c^d mod n

上下两个式子合并

c^d = ((m2−m1)*p−1 mod q)p+m1
m ≡ c^d mod n

最后可以有

m≡(((m2−m1)*p−1 mod q)p+m1) mod n

只剩最后一步了

m1≡cd mod q
m2≡cd mod p

m1和m2怎么求

d≡dp mod (p−1)
d≡dq mod (q−1)

那么分别带入

m1≡cdq mod (q−1) mod q
m2≡cdp mod (p−1) mod p

费马小定理即假如p是质数，且gcd(a,p)=1
a^(p−1)≡1 mod p

所以如果我们有等式

d=dp+k*(p−1)

直接带入
m2≡c^dp+k*(p−1) mod p

这里的指数，我们拆开，为
m2≡c^dp*ck*(p−1) mod p

ck*(p−1)≡1 mod p

因为p是大素数，显然和c互素所以可以直接得到
m2≡cd^p mod p

那么m1根据对称性也可以同理得到

m1≡cd^q mod q

故此，我们现在拥有了所有条件，下面归纳一下为

m1≡cd^q mod q
m2≡cd^p mod p
m≡(((m2−m1)*p−1 mod q)p+m1) mod n
但用的明明是m≡(((m2−m1)*p−1 mod q)p+m1)

import gmpy2
import libnum
from Crypto.Util.number import long_to_bytes,bytes_to_long

p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852

def decrypt(dp, dq, p, q, c):
    InvQ = gmpy2.invert(q, p)
    mp = pow(c, dp, p)
    mq = pow(c, dq, q)
    m = (((mp - mq) * InvQ) % p) * q + mq
    m = (((mp-mq)*InvQ)%p)*q+mq
    #print(mp - mq)
    print(libnum.n2s(int(m)).decode())
decrypt(dp, dq, p, q, c)
求解q关于p的逆元InvQ。这一步的目的是为后面的计算提供一个辅助值，根据扩展欧几里得算法，只有当p和q互质时，InvQ存在。
分别使用dp和dq对密文c进行模p和模q的解密，得到mp和mq。
计算明文m，首先计算((mp - mq) * InvQ) % p，这一步的目的是将两个模数下的解密结果合并成一个值，再乘以q加上mq，得到最终的明文m。

世上无难事

一些无规律的字符串，首先猜测是凯撒或者替换密码，但是经过凯撒密码各种偏移量穷举，都没有找到有意义的flag，因此推测为替换，打开quipqiup进行破解

Unencode

UUencode

http://web.chacuo.net/charsetuuencode

[AFCTF2018]Morse

提交flag发现错误，突然发现61的ascii对应a 66的ascii对应f
与题目afctf对应，16进制转ascii得到flag
在这里插入图片描述

还原大师

E9032994DABAC08080091151380478A2

#还原md5
import hashlib

k = 'TASC?O3RJMV?WDJKX?ZM'
for i in range(26):
    temp1 = k.replace('?',str(chr(65+i)),1)
    for j in range(26):
        temp2 = temp1.replace('?',chr(65+j),1)
        for n in range(26):
            temp3 = temp2.replace('?',chr(65+n),1)
            s = hashlib.md5(temp3.encode('utf8')).hexdigest().upper()
            if s[:4] == 'E903' and s[7:11] == '4DAB':
                print (s)

异性相吸

1 2	#key.txt asadsasdasdasdasdasdasdasdasdasdqwesqf

#密文.txt

二进制读出异或

miwen = open("E:\\密文.txt",'rb').read()
key = open("E:\\key.txt",'rb').read()
flag = ''
for i in range(0,len(miwen)):
    str = list(miwen)[i] ^ list(key)[i]
    flag += chr(str)
print(flag)

RSA

密钥公钥读取

from Crypto.PublicKey import RSA
import libnum
import rsa
import base64
import gmpy2
from Crypto.Util.number import bytes_to_long, long_to_bytes
with open("pub.key", "r") as f:
    key = RSA.import_key(f.read())
    print(key.e)
    print(key.n)
#Public RSA key at 0x2EFEEFB16A0
n =86934482296048119190666062003494800588905656017203025617216654058378322103517
e =65537
q=285960468890451637935629440372639283459
p=304008741604601924494328155975272418463
phi=(p-1)*(q-1)
d = gmpy2.invert(e,phi)
with open('flag.enc', 'rb') as file:
    data = bytes_to_long(file.read())
    res = long_to_bytes(pow(data, d, n))
    print(res)

RSAROOL

{920139713,19}–>>{n,e}

from Crypto.PublicKey import RSA
import libnum
import rsa
import base64
import gmpy2
from Crypto.Util.number import bytes_to_long, long_to_bytes

p=18443
q=49891
n=920139713
e=19
phi=(p-1)*(q-1)
d = gmpy2.invert(e,phi)
flag =b''
with open('1.txt','r') as f:
    for c in f:

        m=gmpy2.powmod(int(c),d,n)
        m1=libnum.n2s(int(m))
        flag += m1

print(flag)

Dangerous RSA-低加密指数小明文攻击

e很小，为低加密指数攻击
①m3<n,也就是说m3=c。
②m3>n，即(m3+i·n)mod n=c（爆破i）

from Crypto.PublicKey import RSA
import libnum
import rsa
import base64
import gmpy2
from Crypto.Util.number import bytes_to_long, long_to_bytes

n=  0x52d483c27cd806550fbe0e37a61af2e7cf5e0efb723dfc81174c918a27627779b21fa3c851e9e94188eaee3d5cd6f752406a43fbecb53e80836ff1e185d3ccd7782ea846c2e91a7b0808986666e0bdadbfb7bdd65670a589a4d2478e9adcafe97c6ee23614bcb2ecc23580f4d2e3cc1ecfec25c50da4bc754dde6c8bfd8d1fc16956c74d8e9196046a01dc9f3024e11461c294f29d7421140732fedacac97b8fe50999117d27943c953f18c4ff4f8c258d839764078d4b6ef6e8591e0ff5563b31a39e6374d0d41c8c46921c25e5904a817ef8e39e5c9b71225a83269693e0b7e3218fc5e5a1e8412ba16e588b3d6ac536dce39fcdfce81eec79979ea6872793
e=  3
c=  0x10652cdfaa6b63f6d7bd1109da08181e500e5643f5b240a9024bfa84d5f2cac9310562978347bb232d63e7289283871efab83d84ff5a7b64a94a79d34cfbd4ef121723ba1f663e514f83f6f01492b4e13e1bb4296d96ea5a353d3bf2edd2f449c03c4a3e995237985a596908adc741f32365
#so,how to get the message?
# phi=(p-1)*(q-1)

k=0
while True:
    m1 = c*k+c
    m,t = gmpy2.iroot(m1,e)
    if t:
        print(m)
        print(k)
        print(libnum.n2s(int(m)))
        break
    k += 1

Cipher

题目描述

1	还能提示什么呢？公平的玩吧（密钥自己找） Dncnoqqfliqrpgeklwmppu 注意：得到的 flag 请包上 flag{} 提交, flag{小写字母}

公平的玩吧

这个就是提示百度翻译一下是Play fair
有一个Play fair解密

在这里插入图片描述
再把得到的
这个转换为小写即可提交。

[GXYCTF2019]CheckIn

ROT47…少见

密码学的心声

ASCLL码八进制三个一组进行转换

flag{ILoveSecurityVeryMuch}

rsa2

刚开始求出d之后MD5一直不对

N = 101991809777553253470276751399264740131157682329252673501792154507006158434432009141995367241962525705950046253400188884658262496534706438791515071885860897552736656899566915731297225817250639873643376310103992170646906557242832893914902053581087502512787303322747780420210884852166586717636559058152544979471
e = 46731919563265721307105180410302518676676135509737992912625092976849075262192092549323082367518264378630543338219025744820916471913696072050291990620486581719410354385121760761374229374847695148230596005409978383369740305816082770283909611956355972181848077519920922059268376958811713365106925235218265173085
d=8920758995414587152829426558580025657357328745839747693739591820283538307445
import hashlib
print(hex(d))
flag = "flag{" + hashlib.md5(hex(d).encode('utf-8')).hexdigest() + "}"
print(hashlib.md5(b'0x13b8f87d588e2aa4a27296cf2898f56ab4c8deb5a1222ec080e23afecaf7f975').hexdigest())

找到原因是因为,加密脚本是python2

python2与python3–hex(d)的结果相差了一个末尾的L所以要再补上一个L

robomunication

将MP3拖入Audacity

…/./.-…/.-…/—/.–/…/.-/-/…/…/-/…/./-.-/./-.–/…/-/…/…/-…/—/—/.–./-…/././.–.

[WUSTCTF2020]佛说：只能四天

用与佛论禅解不出来，“新约全书”可能是提示吧，最后用新约佛论禅解得(注意前面要加上“佛曰：”)：
社会主义核心价值观编码，解得：

RLJDQTOVPTQ6O6duws5CD6IB5B52CC57okCaUUC3SO4OSOWG3LynarAVGRZSJRAEYEZ_ooe_doyouknowfence

字符串末提示栅栏密码，起初将整个字符串放进去解码发现怎么也得不到有用的信息。。。实际上要先把后面的提示信息去掉，再解码。也即RLJDQTOVPTQ6O6duws5CD6IB5B52CC57okCaUUC3SO4OSOWG3LynarAVGRZSJRAEYEZ_ooe用4位栅栏密码，栅栏密码解密结果为：

R5UALCUVJDCGD63RQISZTBOSO54JVBORP5SAT2OEQCWY6CGEO53Z67L_doyouknowCaesar

根据以上的经验，需对R5UALCUVJDCGD63RQISZTBOSO54JVBORP5SAT2OEQCWY6CGEO53Z67L用凯撒密码移位解密。同时，这里只有大写字母和2~7的数字，且提示中说明凯撒不是最后一步，因此得到的结果还需Base32解码。验证知，凯撒密码移位数为3，结果是：

O5RXIZRSGAZDA63ONFPWQYLPL54GSYLOM5PXQ2LBNZTV6ZDBL53W67I

这个可以通过Base32解码得到：
wctf2020{ni_hao_xiang_xiang_da_wo}

1	https://www.cnblogs.com/vict0r/p/13529640.html

[ACTF新生赛2020]crypto-rsa0

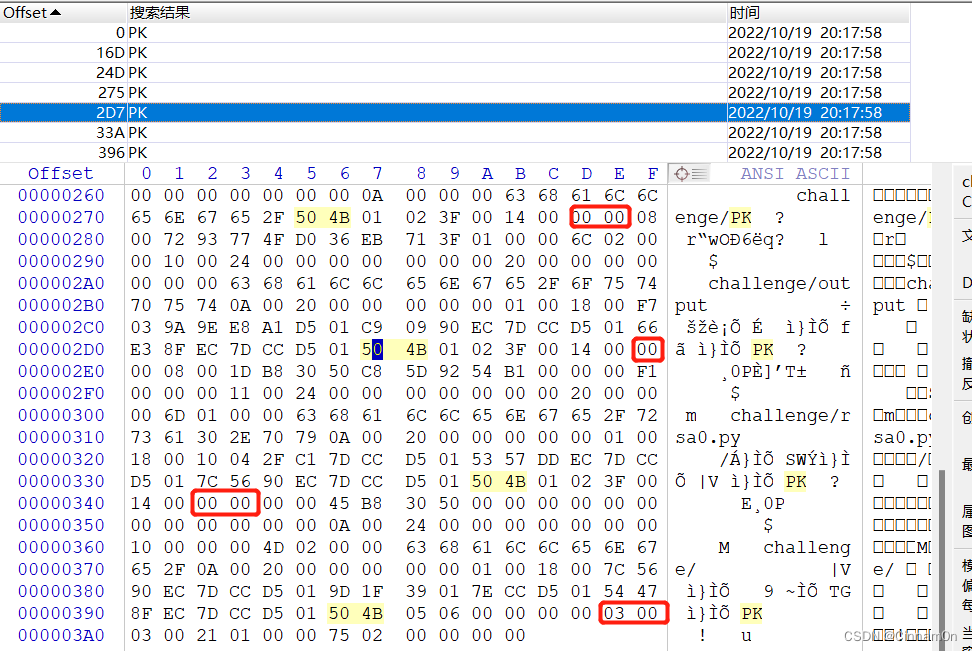
   接下来我们尝试打开challenge时发现提示我们有密码，在hint中已经提醒我们本题采用了伪加密。

概念：

ZIP伪加密 ，一个ZIP文件由三个部分组成：

压缩源文件数据区+压缩源文件目录区+压缩源文件目录结束标志。 

伪加密原理：zip伪加密是在文件头的加密标志位做修改，进而再打开文件时识被别为加密压缩

包。 一般来说，文件各个区域开头就是50 4B，然后后面两个字节是版本，再后面两个就是判断

是否有加密的关键了。

关于伪加密可以去大致了解一下：(2条消息) 压缩包伪加密原理_每天都要努力哇的博客-CSDN博客_压缩包伪加密

解决方法是打开Winhex，遇到504B0304，把其的第3、4个byte改成0000，遇到504B0102，把其的第5、6个byte改成0000即可破解伪加密。

利用搜索功能可以快很多

原文链接：https://blog.csdn.net/shshss64/article/details/127193342

rot

加深一下对rot的认识,

ROT5、ROT13、ROT18、ROT47 编码是一种简单的码元位置顺序替换暗码。此类编码具有可逆性，可以自我解密，主要用于应对快速浏览，或者是机器的读取，而不让其理解其意。
 
ROT5 是 rotate by 5 places 的简写，意思是旋转5个位置，其它皆同。下面分别说说它们的编码方式：
ROT5：只对数字进行编码，用当前数字往前数的第5个数字替换当前数字，例如当前为0，编码后变成5，当前为1，编码后变成6，以此类推顺序循环。
ROT13：只对字母进行编码，用当前字母往前数的第13个字母替换当前字母，例如当前为A，编码后变成N，当前为B，编码后变成O，以此类推顺序循环。
ROT18：这是一个异类，本来没有，它是将ROT5和ROT13组合在一起，为了好称呼，将其命名为ROT18。
ROT47：对数字、字母、常用符号进行编码，按照它们的ASCII值进行位置替换，用当前字符ASCII值往前数的第47位对应字符替换当前字符，例如当前为小写字母z，编码后变成大写字母K，当前为数字0，编码后变成符号_。用于ROT47编码的字符其ASCII值范围是33－126，具体可参考ASCII编码。

但是有大于 127 的数字存在，所以要先处理。

参考rot原理，将所有的数字 -13 后，再转ascii码

s = ‘83 89 78 84 45 86 96 45 115 121 110 116 136 132 132 132 108 128 117 118 134 110 123 111 110 127 108 112 124 122 108 118 128 108 131 114 127 134 108 116 124 124 113 108 76 76 76 76 138 23 90 81 66 71 64 69 114 65 112 64 66 63 69 61 70 114 62 66 61 62 69 67 70 63 61 110 110 112 64 68 62 70 61 112 111 112’
l = s.split(" ")
for i in l:
print(chr(int(i)-13),end=‘’)
输出结果：

FLAG IS flag{www_shiyanbar_com_is_very_good_???}
MD5:38e4c352809e150186920aac37190cbc
看样子要爆破后四位，

demo='flag{www_shiyanbar_com_is_very_good_'
check = '38e4c352809e150186920aac37190cbc'
 
for i in range(32,126):
    for j in range(32,126):
        for k in range(32,126):
            for m in range(32,126):
                tmp = demo + chr(i) + chr(j) + chr(k) + chr(m) + '}'
                hash = hashlib.md5(tmp.encode('utf8')).hexdigest()
                if check == hash:
                    print(tmp)
                    exit()

[GWCTF 2019]BabyRSA

import gmpy2
from Crypto.Util.number import bytes_to_long, long_to_bytes
from sympy import symbols, solve
n=636585149594574746909030160182690866222909256464847291783000651837227921337237899651287943597773270944384034858925295744880727101606841413640006527614873110651410155893776548737823152943797884729130149758279127430044739254000426610922834573094957082589539445610828279428814524313491262061930512829074466232633130599104490893572093943832740301809630847541592548921200288222432789208650949937638303429456468889100192613859073752923812454212239908948930178355331390933536771065791817643978763045030833712326162883810638120029378337092938662174119747687899484603628344079493556601422498405360731958162719296160584042671057160241284852522913676264596201906163
m1=90009974341452243216986938028371257528604943208941176518717463554774967878152694586469377765296113165659498726012712288670458884373971419842750929287658640266219686646956929872115782173093979742958745121671928568709468526098715927189829600497283118051641107305128852697032053368115181216069626606165503465125725204875578701237789292966211824002761481815276666236869005129138862782476859103086726091860497614883282949955023222414333243193268564781621699870412557822404381213804026685831221430728290755597819259339616650158674713248841654338515199405532003173732520457813901170264713085107077001478083341339002069870585378257051150217511755761491021553239
m2=487443985757405173426628188375657117604235507936967522993257972108872283698305238454465723214226871414276788912058186197039821242912736742824080627680971802511206914394672159240206910735850651999316100014691067295708138639363203596244693995562780286637116394738250774129759021080197323724805414668042318806010652814405078769738548913675466181551005527065309515364950610137206393257148357659666687091662749848560225453826362271704292692847596339533229088038820532086109421158575841077601268713175097874083536249006018948789413238783922845633494023608865256071962856581229890043896939025613600564283391329331452199062858930374565991634191495137939574539546
e = 0x10001
p=797862863902421984951231350430312260517773269684958456342860983236184129602390919026048496119757187702076499551310794177917920137646835888862706126924088411570997141257159563952725882214181185531209186972351469946269508511312863779123205322378452194261217016552527754513215520329499967108196968833163329724620251096080377747699
q=797862863902421984951231350430312260517773269684958456342860983236184129602390919026048496119757187702076499551310794177917920137646835888862706126924088411570997141257159563952725882214181185531209186972351469946269508511312863779123205322378452194261217016552527754513215520329499967108196968833163329724620251096080377748737
phi =(q-1)*(p-1)

d = gmpy2.invert(e,phi)
m1=pow(m1,d,n)
m2=pow(m2,d,n)
f1,f2=symbols('f1 f2')
eq1=f1+f2-2732509502629189160482346120094198557857912754
eq2=pow(f1, 3) + pow(f2, 3)-5514544075236012543362261483183657422998274674127032311399076783844902086865451355210243586349132992563718009577051164928513093068525554
s = solve((eq1,eq2),(f1,f2))
print(s)
f1=1141553212031156130619789508463772513350070909
f2=1590956290598033029862556611630426044507841845
print(long_to_bytes(f2))
print(long_to_bytes(f1))
#GWHT{f709e0e2cfe7e530ca8972959a1033b2}

[MRCTF2020]古典密码知多少

猪圈密码+标准银河字母+圣堂武士

FGCPFLIRTUASYON

[HDCTF2019]bbbbbbrsa

p=177077389675257695042507998165006460849
q=211330365658290458913359957704294614589

n = 37421829509887796274897162249367329400988647145613325367337968063341372726061
c = '==gMzYDNzIjMxUTNyIzNzIjMyYTM4MDM0gTMwEjNzgTM2UTN4cjNwIjN2QzM5ADMwIDNyMTO4UzM2cTM5kDN2MTOyUTO5YDM0czM3MjM'
c = 2373740699529364991763589324200093466206785561836101840381622237225512234632
phi = (q-1)*(p-1)
for e in range(50000,70000):
   if gmpy2.gcd(e,phi) == 1:
      d = gmpy2.invert(e ,phi)
      m = pow(c,d,n)
      if 'flag' in str(long_to_bytes(m)):
                    print(long_to_bytes(m))

不使用if gmpy2.gcd(e,phi) == 1: 直接使用if gmpy2.invert(e,phi) == 1:的话会报错

999 666 88 2 777 33 7777 6 2 777 8 8 44 2 8 8 44 444 7777
 y   u   o a   r  e      
5 88 7777 8 2 7 444 33 222 33 666 333 222 2 55 33

[BJDCTF2020]RSA

只有一点

1 2	print c,n 输出的c,n中间会有一个空格

import gmpy2,libnum
from Crypto.Util.number import bytes_to_long, long_to_bytes

from gmpy2 import invert,gcd,iroot
from Crypto.Util.number import *
from binascii import a2b_hex,b2a_hex
from sympy import symbols, solve
import base64

c1 = 12641635617803746150332232646354596292707861480200207537199141183624438303757120570096741248020236666965755798009656547738616399025300123043766255518596149348930444599820675230046423373053051631932557230849083426859490183732303751744004874183062594856870318614289991675980063548316499486908923209627563871554875612702079100567018698992935818206109087568166097392314105717555482926141030505639571708876213167112187962584484065321545727594135175369233925922507794999607323536976824183162923385005669930403448853465141405846835919842908469787547341752365471892495204307644586161393228776042015534147913888338316244169120
n1 = 13508774104460209743306714034546704137247627344981133461801953479736017021401725818808462898375994767375627749494839671944543822403059978073813122441407612530658168942987820256786583006947001711749230193542370570950705530167921702835627122401475251039000775017381633900222474727396823708695063136246115652622259769634591309421761269548260984426148824641285010730983215377509255011298737827621611158032976420011662547854515610597955628898073569684158225678333474543920326532893446849808112837476684390030976472053905069855522297850688026960701186543428139843783907624317274796926248829543413464754127208843070331063037
c2 = 979153370552535153498477459720877329811204688208387543826122582132404214848454954722487086658061408795223805022202997613522014736983452121073860054851302343517756732701026667062765906277626879215457936330799698812755973057557620930172778859116538571207100424990838508255127616637334499680058645411786925302368790414768248611809358160197554369255458675450109457987698749584630551177577492043403656419968285163536823819817573531356497236154342689914525321673807925458651854768512396355389740863270148775362744448115581639629326362342160548500035000156097215446881251055505465713854173913142040976382500435185442521721
n2 = 12806210903061368369054309575159360374022344774547459345216907128193957592938071815865954073287532545947370671838372144806539753829484356064919357285623305209600680570975224639214396805124350862772159272362778768036844634760917612708721787320159318432456050806227784435091161119982613987303255995543165395426658059462110056431392517548717447898084915167661172362984251201688639469652283452307712821398857016487590794996544468826705600332208535201443322267298747117528882985955375246424812616478327182399461709978893464093245135530135430007842223389360212803439850867615121148050034887767584693608776323252233254261047
p =gmpy2.gcd(n1,n2)
q1 = n1//p
q2 = n2//p

k = 'BJD'
e=0
n=0

for e in range(100000):
    c1 = 12641635617803746150332232646354596292707861480200207537199141183624438303757120570096741248020236666965755798009656547738616399025300123043766255518596149348930444599820675230046423373053051631932557230849083426859490183732303751744004874183062594856870318614289991675980063548316499486908923209627563871554875612702079100567018698992935818206109087568166097392314105717555482926141030505639571708876213167112187962584484065321545727594135175369233925922507794999607323536976824183162923385005669930403448853465141405846835919842908469787547341752365471892495204307644586161393228776042015534147913888338316244169120
    n1 = 13508774104460209743306714034546704137247627344981133461801953479736017021401725818808462898375994767375627749494839671944543822403059978073813122441407612530658168942987820256786583006947001711749230193542370570950705530167921702835627122401475251039000775017381633900222474727396823708695063136246115652622259769634591309421761269548260984426148824641285010730983215377509255011298737827621611158032976420011662547854515610597955628898073569684158225678333474543920326532893446849808112837476684390030976472053905069855522297850688026960701186543428139843783907624317274796926248829543413464754127208843070331063037
    c2 = 979153370552535153498477459720877329811204688208387543826122582132404214848454954722487086658061408795223805022202997613522014736983452121073860054851302343517756732701026667062765906277626879215457936330799698812755973057557620930172778859116538571207100424990838508255127616637334499680058645411786925302368790414768248611809358160197554369255458675450109457987698749584630551177577492043403656419968285163536823819817573531356497236154342689914525321673807925458651854768512396355389740863270148775362744448115581639629326362342160548500035000156097215446881251055505465713854173913142040976382500435185442521721
    n2 = 12806210903061368369054309575159360374022344774547459345216907128193957592938071815865954073287532545947370671838372144806539753829484356064919357285623305209600680570975224639214396805124350862772159272362778768036844634760917612708721787320159318432456050806227784435091161119982613987303255995543165395426658059462110056431392517548717447898084915167661172362984251201688639469652283452307712821398857016487590794996544468826705600332208535201443322267298747117528882985955375246424812616478327182399461709978893464093245135530135430007842223389360212803439850867615121148050034887767584693608776323252233254261047
    p = gmpy2.gcd(n1, n2)
    q1 = n1 // p
    q2 = n2 // p
    phi = (p - 1) * (q1 - 1)
    phi1 = (p - 1) * (q2 - 1)
    if gmpy2.gcd(e,phi) == 1:
        if gmpy2.gcd(e, phi1) == 1:
            d1 = gmpy2.invert(e, phi)
            d2 = gmpy2.invert(e, phi1)
            m1 = gmpy2.powmod(c1,d1,n1)
            m2 =pow(c2,d2,n2)
            if k in str(libnum.n2s(int(m2))):
                print(libnum.n2s(int(m1)))
                print(libnum.n2s(int(m2)))

RSA4

低加密指数广播攻击

import gmpy2
import libnum

# n1,n2,n3......两两互质
n1 = int(
    '331310324212000030020214312244232222400142410423413104441140203003243002104333214202031202212403400220031202142322434104143104244241214204444443323000244130122022422310201104411044030113302323014101331214303223312402430402404413033243132101010422240133122211400434023222214231402403403200012221023341333340042343122302113410210110221233241303024431330001303404020104442443120130000334110042432010203401440404010003442001223042211442001413004',
    5)
c1 = int(
    '310020004234033304244200421414413320341301002123030311202340222410301423440312412440240244110200112141140201224032402232131204213012303204422003300004011434102141321223311243242010014140422411342304322201241112402132203101131221223004022003120002110230023341143201404311340311134230140231412201333333142402423134333211302102413111111424430032440123340034044314223400401224111323000242234420441240411021023100222003123214343030122032301042243',
    5)

n2 = int(
    '302240000040421410144422133334143140011011044322223144412002220243001141141114123223331331304421113021231204322233120121444434210041232214144413244434424302311222143224402302432102242132244032010020113224011121043232143221203424243134044314022212024343100042342002432331144300214212414033414120004344211330224020301223033334324244031204240122301242232011303211220044222411134403012132420311110302442344021122101224411230002203344140143044114',
    5)
c2 = int(
    '112200203404013430330214124004404423210041321043000303233141423344144222343401042200334033203124030011440014210112103234440312134032123400444344144233020130110134042102220302002413321102022414130443041144240310121020100310104334204234412411424420321211112232031121330310333414423433343322024400121200333330432223421433344122023012440013041401423202210124024431040013414313121123433424113113414422043330422002314144111134142044333404112240344',
    5)

n3 = int(
    '332200324410041111434222123043121331442103233332422341041340412034230003314420311333101344231212130200312041044324431141033004333110021013020140020011222012300020041342040004002220210223122111314112124333211132230332124022423141214031303144444134403024420111423244424030030003340213032121303213343020401304243330001314023030121034113334404440421242240113103203013341231330004332040302440011324004130324034323430143102401440130242321424020323',
    5)
c3 = int(
    '10013444120141130322433204124002242224332334011124210012440241402342100410331131441303242011002101323040403311120421304422222200324402244243322422444414043342130111111330022213203030324422101133032212042042243101434342203204121042113212104212423330331134311311114143200011240002111312122234340003403312040401043021433112031334324322123304112340014030132021432101130211241134422413442312013042141212003102211300321404043012124332013240431242',
    5)
e = 3
n = [n1, n2, n3]
c = [c1, c2, c3]
def GCRT(m, a):
    assert (len(m) == len(a))
    curm, cura = m[0], a[0]
    for m, a in zip(m[1:], a[1:]):
        d = gmpy2.gcd(curm, m)
        c = a - cura
        assert (c % d == 0)
        K = c // d * gmpy2.invert(curm // d, m // d)
        cura += curm * K
        curm = curm * m // d
    return cura % curm
n = [n1, n2, n3]
c = [c1, c2, c3]
mm = libnum.solve_crt(c, n)
print(mm)
for e in range(1, 20):
    m, t = gmpy2.iroot(mm, e)
    if t:
        print(m)
        print(libnum.n2s(int(m)))

[MRCTF2020]keyboard

刚开始得到的mobilephond但是一直不对,

或许是根据英文自己再进行更改的吧mobilephone

传感器

5555555595555A65556AA696AA6666666955
这是某压力传感器无线数据包解调后但未解码的报文(hex)

已知其ID为0xFED31F，请继续将报文完整解码，提交hex。

提示1：曼联

曼联？曼彻斯特！

曼彻斯特编码（Manchester Encoding），也叫做相位编码（ Phase Encode，简写PE），是一个同步时钟编码技术，被物理层使用来编码一个同步位流的时钟和数据。它在以太网媒介系统中的应用属于数据通信中的两种位同步方法里的自同步法（另一种是外同步法），即接收方利用包含有同步信号的特殊编码从信号自身提取同步信号来锁定自己的时钟脉冲频率，达到同步目的。

1	IEEE 802.4（令牌总线）和低速版的IEEE 802.3（以太网）中规定, 按照这样的说法, 01电平跳变表示1, 10的电平跳变表示0。

思路

根据 01->1 , 10->0 ,可得到:

0101->11
0110->10
1010->00
1001->01

5555555595555A65556AA696AA6666666955`十六进制转为二进制得到:
`11111111 11111111 01111111 11001011 11111000 00100110 00001010 10101010 10011111`
bin->hex，对比ID并不重合，根据八位倒序传输协议将二进制每八位reverse，转hex即可
`FFFFFED31F645055F9

百度可基本了解它的编码过程，但没有在线网站来解密，那么只能使用脚本解密

cipher='5555555595555A65556AA696AA6666666955'
def iee(cipher):
    tmp=''
    for i in range(len(cipher)):
        a=bin(eval('0x'+cipher[i]))[2:].zfill(4)#补齐四位方便取1和3位
        tmp=tmp+a[1]+a[3]#加上1和3位，就是应用了802.3的規則，或者定义一个字典替换也可以
        print(tmp)
    plain=[hex(int(tmp[i:i+8][::-1],2))[2:] for i in range(0,len(tmp),8)]
    print(''.join(plain).upper())

iee(cipher)
#数据由5、6、9、a组成

这里学习一下曼彻斯特编码在

曼彻斯特编码

参考链接

链接里面还有更多例题

1	https://blog.csdn.net/qq_38154820/article/details/123288289

通过对数字信号进行编码来表示数据不归零编码、曼切斯特编码、差分曼切斯特编码都是其编码方式

差分曼彻斯特编码是一种使用中位转变来计时的编码方案。数据通过在数据位开始处加一转变来表示。令牌环局域网就利用差分曼彻斯特编码方案。在每个时钟周期的中间都有一次电平跳变，这个跳变做同步之用。在每个时钟周期的起始处：跳变则说明该比特是0，不跳变则说明该比特是1。差分曼彻斯特编码的优点为：收发双方可以根据编码自带的时钟信号来保持同步，无需专门传递同步信号的线路，因此成本低；缺点为：实现技术复杂。

曼彻斯特编码（Manchester Encoding），也叫做相位编码(PE)，是一个同步时钟编码技术，被物理层使用来编码一个同步位流的时钟和数据。曼彻斯特编码被用在以太网媒介系统中。曼彻斯特编码提供一个简单的方式给编码简单的二进制序列而没有长的周期没有转换级别，因而防止时钟同步的丢失，或来自低频率位移在贫乏补偿的模拟链接位错误。在这个技术下，实际上的二进制数据被传输通过这个电缆，不是作为一个序列的逻辑1或0来发送的（技术上叫做反向不归零制(NRZ)）。相反地，这些位被转换为一个稍微不同的格式，它通过使用直接的二进制编码有很多的优点。

差分曼彻斯特编码，每位中间的跳变仅提供时钟定时，而用每位开始时有无跳变表示"0"或"1"，有跳变为"0"，无跳变为"1"。

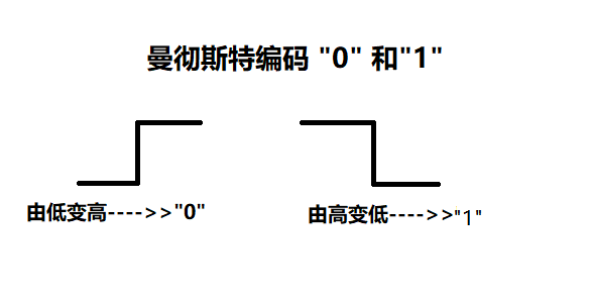
曼彻斯特编码的编码规则是:在信号位中电平从低到高跳变表示1，在信号位中电平从高到低跳变表示0。

这个图就单独的表示曼彻斯特编码的0,1原理图从低到高就是0，从高到低就是1

看曼彻斯特就简单的分成一段一段看他上升还是下降就可以表示出来

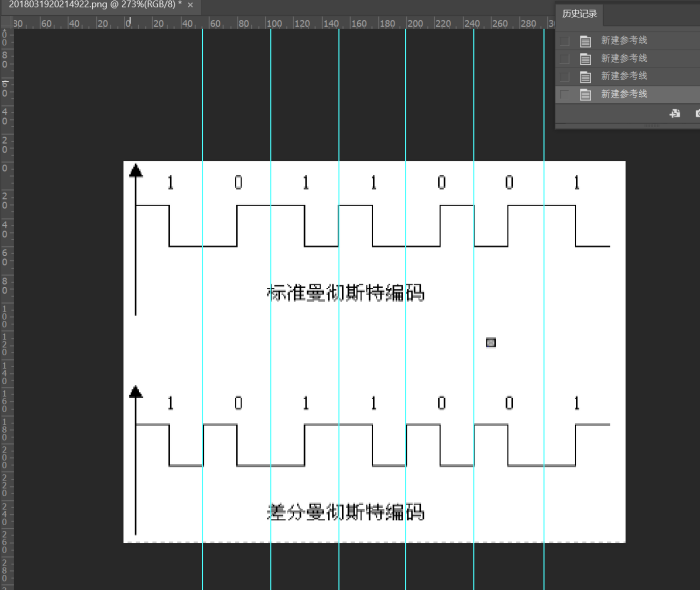
而差分曼彻斯特要看他前一个信号的值，比如这图里第一个就是不跳就用1表示，第二个信号从底下升到高处就跳了表示0，第三个也是不跳用1表示，第4个同理也是1，第5个跳了就是0。而差分的意思应该就是要把一段内拆成两段只看前一段，而后一半是用来同步时钟用的，顺便可以传输下一个数据来表示是否有跳

再来看下三种信号的区别

在来说下802.3曼彻斯特和标准曼彻斯特的区别，就是编码后的字符的区别。第一种G. E. Thomas, Andrew S. Tanenbaum1949年提出的，它规定0是由低-高的电平跳变表示，1是高-低的电平跳变。按此规则有：

编码0101（即0x5），表示原数据为00；

编码1001（0x9）表示10；

编码0110（0x6）表示01；

编码1010（0xA）表示11。

第二种IEEE 802.4（令牌总线）和低速版的IEEE 802.3（以太网）中规定, 按照这样的说法, 低-高电平跳变表示1, 高-低的电平跳变表示0。

编码0101（0x5）表示11；

编码1001（0x9）表示01；

编码0110（0x6）表示10；

编码1010（0xA）表示00