定理
费马小定理
费马小定理是数论中的一个重要定理,在1636年提出.
在学之前先了解一下
剩余类:,亦称同余类,是一种数学的用语,为数论的基本概念之一.设模为n,则根据余数可将所有的整数分为n类,把所有与整数a模n同余的整数构成的集合叫做模n的一个剩余类，记作[a]。并把a叫作剩余类[a]的一个代表元。
完全剩余系:从每个剩余系中各取一个数,得到一个由n个数组成的集合，叫做模n的一个完全剩余系。完全剩余系常用于数论中存在性证明。
同余式:a和b被m除时有相同的余数。 同余式的性质
如果p是一个质数,而整数a不是p的倍数,则
a^(p-1)≡1 mod (p)
两边同乘 a,得:
a^p≡a mod (p)
当然这是a<p的情况
推导
引理1
若a,b,c为任意三个整数,m为正整数,且(m,c)=1,则
当a*c≡b*c mod (m)时
有a≡b mod (m)
证明
a*b=b*c mod (m)可得:
ac-bc≡0 mod (m)可得:
c*(a-b) ≡ 0 mod (m)
**因为(m,c)=1即m,c互质,**c可以约去,
a-b ≡ 0 mod (m)可得:
a≡b mod (m)
引理2
设m是以一个整数且m>1,b是以一个整数且(m,b)=1 如果a[1],a[2],a[3],a[4],…a[m]是模m的一个完全剩余系 ，则b·a[1],b·a[2],b·a[3],b·a[4],…b·a[m]也构成模m的一个完全剩余系。
所以b·a[1],b·a[2],b·a[3],b·a[4],…b·a[m]构成模m的一个完全剩余系。
构造素数p的完全剩余系
由完全剩余系的性质，
即(p-1)! ≡ (p-1)! * a^(p-1) mod (p)
易知((p-1!),p)=1,同余式两边可约去(p-1)!,得到:
/这里不懂的话,可以去看看同余式 /
a**(p-1) ≡ 1 mod (p)
这样就证明了费马小定理。
另外
两边同乘a:
a^p ≡ a mod (p)
这个公式就可以用到RSA解密算法
定理意义
费马小定理是初等数论四大定理（威尔逊定理 ，欧拉定理 （数论中的欧拉定理），中国剩余定理(又称孙子定理 ），费马小定理）之一，在初等数论 中有着非常广泛和重要的应用。实际上，它是欧拉定理的一个特殊情况（即
费马大定理
当整数n>2时，关于x,y,z的方程
虽然我这个暂时没用到,但是看了定理的证明经历,真的有一种,我站在巨人的肩膀上的感觉
欧拉定理
在数论中，欧拉定理（也称费马-欧拉定理或欧拉φ函数定理）是一个关于同余的性质。
设a,m∈N+, 且gcd(a,m)=1, 则我们有:有aΦ(n) = 1(mod n).
即对于任何互质的正整数a和n,有aΦ(n) = 1(mod n)
φ(n) 为欧拉函数。欧拉定理得名于瑞士数学家莱昂哈德·欧拉。
欧拉定理实际上是费马小定理的推广。
威尔逊定理
在初等数论中，威尔逊定理给出了判定一个自然数是否为质数的充分必要条件。即：当且仅当p为质数时：
(p-1)! ≡ -1 mod (p)
但是由于阶乘是呈爆炸增长的,其结论对于实际操作意义不大.
证明
充分性
如果p不是素数,
当p=4时:
显然(p-1)! ≡ 6 ≡ 2 mod (p)
当p>4时,
若p不是完全平方数 则存在两个不等的因数a,b使得ab=p,则(p-1)! ≡ nab ≡ 0 mod (p)
若p是完全 平方数即p=k^2,因为p>4,所以k>2,(k,2k)<p ,(p-1)! ≡ n(k*2k) ≡ 2n*k^2 ≡ 0 mod (p)
必要性
若p是素数,取集合A={1,2,3,…,p-1};则A构成模p乘法的简化剩余系,即任意i∈A,存在j∈A,使得:
(i*j) ≡ 1 mod (p)那么A中的元素是不是恰好两两配对呢? 不一定,但只需考虑这种情况
x^2 ≡ 1 mod (p)
解得:
x ≡ 1 mod (p) 或 x ≡ p-1 mod (p)
其余两两配对;故而
(p-1)! ≡ 1*(p-1) ≡ -1 mod (p)
中国剩余定理(孙子定理/GRT)
定义
用现代数学的语言来说明的话，中国剩余定理给出了以下的一元线性同余方程 组：
说明
假设整数m1,m2,…,mn其中任两数互质,则对任意的整数:a1,a2,…,an,方程组**(S)**有解,并且通解可以用如下方式构造得到:
设$M=m_1×m_2×\dots×m_n=\prod\limits_{i=1}^{n} m_i$是整数m 1,m 2, … ,m n的乘积，并设$m_1,m_2,…,m_n$是除了m i以外的n - 1个整数的乘积。
设 $t_i=M_i^{-1}$ 为 $M_i$为$m_i$ 模 $m_i$的数论倒数 :$t_iM_i \equiv 1 \pmod {m_i},\forall i \in {1,2,…,n}$
方程组**(S)** 的通解形式为$x=a_1t_1M_1+a_2t_2M_2+\dots+a_nt_nM_n+kM=kM+\sum\limits_{i=1}^{n}a_it_iM_i,\quad k\in \mathbb{Z}$在模$M$的意义下，方程组**(S)** 只有一个解：
模不两两互质的同余式组可化为模两两互质的同余式组,再用孙子定理直接求解
在《孙子算经》中有这样一个问题：“今有物不知其数，三三数之剩二（除以3余2），五五数之剩三（除以5余3），七七数之剩二（除以7余2），问物几何？”这个问题称为“孙子问题”，该问题的一般解法国际上称为“中国剩余定理”。
1 2 3 4 5 6 7 8 9 10 11 12 def chinese_remainder (modulus, remainders ): Sum = 0 prod = reduce(lambda a, b: a*b, modulus) for m_i, r_i in zip (modulus, remainders): p = prod // m_i Sum += r_i * (inverse_mod(p,m_i)*p) return Sum % prod chinese_remainder([3 ,5 ,7 ],[2 ,3 ,2 ]) /** Lazzaro @ https://lazzzaro.github.io */
扩展中国剩余定理（扩展CRT / ExCRT）
中国剩余定理是用来解同余方程组的，它要求 m1,m2,…,mn 其中两两互质。
模不两两互质 的同余式组可化为模两两互质的同余式组，再用中国剩余定理直接求解。
形式
给定 n 组非负整数 mi,ai 求解关于 x 的方程组的最小非负整数解。
解法
扩展中国剩余定理的方法和中国剩余定理关系不大，我们贪心处理前 i−1 项，然后合并当前方程。
将每个方程拆成若干个方程
对每个质数 p ，合并对应的$a+b=1所有方程，从而转化为模数两两互质的情形。若合并过程中出现矛盾，则原方程组无解。
RSA考察点
整数RSA加解密原理
基于多项式上的RSA加密
多项式RSA倒推
在RSA的基础原理上将多项式带入整数进行分析.
采用sage语言解题
我们可以利用sage中的factor()函数分解多项式N得到两个不可约多项式p,q,
1 2 3 4 5 6 7 p = 40031 P = PolynomialRing(Zmod(p), name = 'x') x = P.gen() n=24096*x^93 + 38785*x^92 + 17489*x^91 + 9067*x^90 + 1034*x^89 + 6534*x^88 + 35818*x^87 + 22046*x^86 + 12887*x^85 + 445*x^84 + 26322*x^83 + 37045*x^82 + 4486*x^81 + 3503*x^80 + 1184*x^79 + 38471*x^78 + 8012*x^77 + 36561*x^76 + 19429*x^75 + 35227*x^74 + 10813*x^73 + 26341*x^72 + 29474*x^71 + 2059*x^70 + 16068*x^69 + 31597*x^68 + 14685*x^67 + 9266*x^66 + 31019*x^65 + 6171*x^64 + 385*x^63 + 28986*x^62 + 9912*x^61 + 10632*x^60 + 33741*x^59 + 12634*x^58 + 21179*x^57 + 35548*x^56 + 17894*x^55 + 7152*x^54 + 9440*x^53 + 4004*x^52 + 2600*x^51 + 12281*x^50 + 22*x^49 + 17314*x^48 + 32694*x^47 + 7693*x^46 + 6567*x^45 + 19897*x^44 + 27329*x^43 + 8799*x^42 + 36348*x^41 + 33963*x^40 + 23730*x^39 + 27685*x^38 + 29037*x^37 + 14622*x^36 + 29608*x^35 + 39588*x^34 + 23294*x^33 + 757*x^32 + 20140*x^31 + 19511*x^30 + 1469*x^29 + 3898*x^28 + 6630*x^27 + 19610*x^26 + 11631*x^25 + 7188*x^24 + 11683*x^23 + 35611*x^22 + 37286*x^21 + 32139*x^20 + 20296*x^19 + 36426*x^18 + 25340*x^17 + 36204*x^16 + 37787*x^15 + 31256*x^14 + 505*x^13 + 27508*x^12 + 20885*x^11 + 32037*x^10 + 31236*x^9 + 7929*x^8 + 27195*x^7 + 28980*x^6 + 11863*x^5 + 16025*x^4 + 16389*x^3 + 570*x^2 + 36547*x + 10451 c=3552*x^92 + 6082*x^91 + 25295*x^90 + 35988*x^89 + 26052*x^88 + 16987*x^87 + 12854*x^86 + 25117*x^85 + 25800*x^84 + 30297*x^83 + 5589*x^82 + 23233*x^81 + 14449*x^80 + 4712*x^79 + 35719*x^78 + 1696*x^77 + 35653*x^76 + 13995*x^75 + 13715*x^74 + 4578*x^73 + 37366*x^72 + 25260*x^71 + 28865*x^70 + 36120*x^69 + 7047*x^68 + 10497*x^67 + 19160*x^66 + 17939*x^65 + 14850*x^64 + 6705*x^63 + 17805*x^62 + 30083*x^61 + 2400*x^60 + 10685*x^59 + 15272*x^58 + 2225*x^57 + 13194*x^56 + 14251*x^55 + 31016*x^54 + 10189*x^53 + 35040*x^52 + 7042*x^51 + 29206*x^50 + 39363*x^49 + 32608*x^48 + 38614*x^47 + 5528*x^46 + 20119*x^45 + 13439*x^44 + 25468*x^43 + 30056*x^42 + 19720*x^41 + 21808*x^40 + 3712*x^39 + 25243*x^38 + 10606*x^37 + 16247*x^36 + 36106*x^35 + 17287*x^34 + 36276*x^33 + 1407*x^32 + 28839*x^31 + 8459*x^30 + 38863*x^29 + 435*x^28 + 913*x^27 + 36619*x^26 + 15572*x^25 + 9363*x^24 + 36837*x^23 + 17925*x^22 + 38567*x^21 + 38709*x^20 + 13582*x^19 + 35038*x^18 + 31121*x^17 + 8933*x^16 + 1666*x^15 + 21940*x^14 + 25585*x^13 + 840*x^12 + 21938*x^11 + 20143*x^10 + 28507*x^9 + 5947*x^8 + 20289*x^7 + 32196*x^6 + 924*x^5 + 370*x^4 + 14849*x^3 + 10780*x^2 + 14035*x + 15327 e=65537 q1, q2 = n.factor()
计算phi以及d
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 p = 40031 P = PolynomialRing(Zmod(p), name = 'x' ) x = P.gen() n=24096 *x^93 + 38785 *x^92 + 17489 *x^91 + 9067 *x^90 + 1034 *x^89 + 6534 *x^88 + 35818 *x^87 + 22046 *x^86 + 12887 *x^85 + 445 *x^84 + 26322 *x^83 + 37045 *x^82 + 4486 *x^81 + 3503 *x^80 + 1184 *x^79 + 38471 *x^78 + 8012 *x^77 + 36561 *x^76 + 19429 *x^75 + 35227 *x^74 + 10813 *x^73 + 26341 *x^72 + 29474 *x^71 + 2059 *x^70 + 16068 *x^69 + 31597 *x^68 + 14685 *x^67 + 9266 *x^66 + 31019 *x^65 + 6171 *x^64 + 385 *x^63 + 28986 *x^62 + 9912 *x^61 + 10632 *x^60 + 33741 *x^59 + 12634 *x^58 + 21179 *x^57 + 35548 *x^56 + 17894 *x^55 + 7152 *x^54 + 9440 *x^53 + 4004 *x^52 + 2600 *x^51 + 12281 *x^50 + 22 *x^49 + 17314 *x^48 + 32694 *x^47 + 7693 *x^46 + 6567 *x^45 + 19897 *x^44 + 27329 *x^43 + 8799 *x^42 + 36348 *x^41 + 33963 *x^40 + 23730 *x^39 + 27685 *x^38 + 29037 *x^37 + 14622 *x^36 + 29608 *x^35 + 39588 *x^34 + 23294 *x^33 + 757 *x^32 + 20140 *x^31 + 19511 *x^30 + 1469 *x^29 + 3898 *x^28 + 6630 *x^27 + 19610 *x^26 + 11631 *x^25 + 7188 *x^24 + 11683 *x^23 + 35611 *x^22 + 37286 *x^21 + 32139 *x^20 + 20296 *x^19 + 36426 *x^18 + 25340 *x^17 + 36204 *x^16 + 37787 *x^15 + 31256 *x^14 + 505 *x^13 + 27508 *x^12 + 20885 *x^11 + 32037 *x^10 + 31236 *x^9 + 7929 *x^8 + 27195 *x^7 + 28980 *x^6 + 11863 *x^5 + 16025 *x^4 + 16389 *x^3 + 570 *x^2 + 36547 *x + 10451 c=3552 *x^92 + 6082 *x^91 + 25295 *x^90 + 35988 *x^89 + 26052 *x^88 + 16987 *x^87 + 12854 *x^86 + 25117 *x^85 + 25800 *x^84 + 30297 *x^83 + 5589 *x^82 + 23233 *x^81 + 14449 *x^80 + 4712 *x^79 + 35719 *x^78 + 1696 *x^77 + 35653 *x^76 + 13995 *x^75 + 13715 *x^74 + 4578 *x^73 + 37366 *x^72 + 25260 *x^71 + 28865 *x^70 + 36120 *x^69 + 7047 *x^68 + 10497 *x^67 + 19160 *x^66 + 17939 *x^65 + 14850 *x^64 + 6705 *x^63 + 17805 *x^62 + 30083 *x^61 + 2400 *x^60 + 10685 *x^59 + 15272 *x^58 + 2225 *x^57 + 13194 *x^56 + 14251 *x^55 + 31016 *x^54 + 10189 *x^53 + 35040 *x^52 + 7042 *x^51 + 29206 *x^50 + 39363 *x^49 + 32608 *x^48 + 38614 *x^47 + 5528 *x^46 + 20119 *x^45 + 13439 *x^44 + 25468 *x^43 + 30056 *x^42 + 19720 *x^41 + 21808 *x^40 + 3712 *x^39 + 25243 *x^38 + 10606 *x^37 + 16247 *x^36 + 36106 *x^35 + 17287 *x^34 + 36276 *x^33 + 1407 *x^32 + 28839 *x^31 + 8459 *x^30 + 38863 *x^29 + 435 *x^28 + 913 *x^27 + 36619 *x^26 + 15572 *x^25 + 9363 *x^24 + 36837 *x^23 + 17925 *x^22 + 38567 *x^21 + 38709 *x^20 + 13582 *x^19 + 35038 *x^18 + 31121 *x^17 + 8933 *x^16 + 1666 *x^15 + 21940 *x^14 + 25585 *x^13 + 840 *x^12 + 21938 *x^11 + 20143 *x^10 + 28507 *x^9 + 5947 *x^8 + 20289 *x^7 + 32196 *x^6 + 924 *x^5 + 370 *x^4 + 14849 *x^3 + 10780 *x^2 + 14035 *x + 15327 e=65537 q, p = n.factor() print (q)print (p)q, p = q[0 ], p[0 ] print (q)print (p)phi = (p**q.degree() - 1 ) * (p**p.degree() - 1 ) assert gcd(e, phi) == 1 d = inverse_mod(e, phi) m = pow (c,d,n) flag = bytes (m.coefficients()) print ("Flag: " , flag.decode())
光滑数
p-1光滑
pollard’s p-1分解算法
如果一个整数的所有素因子都不大与B,我们称这个数为B-Smooth数
设 p-1 是B-Smooth的,可设 $p-1=p_1p_2 \cdots p_n(\forall 1 \leq i \leq n,p_i \leq B)$
若p_1,p_2, \cdots ,p_n两两不同，则$p_1p_2 \cdots p_n \mid B! \Rightarrow (p-1) \mid B! \Rightarrow B!=k(p-1)$
因此 $a^{B!} \equiv a^{k(p-1)} \equiv 1 \pmod p$,假设$N=pq$，计算$\gcd(a^{B!}-1，N)$，只要结果大于 0 小于 $N$，那么结果就为 $p$。
1 2 3 4 5 6 7 8 9 10 11 12 13 from gmpy2 import *a = 2 k = 2 N = while True : a = powmod(a, k, N) res = gcd(a-1 , N) if res != 1 and res != N: q = N // res print ("p =" ,res) print ("q =" ,q) break k += 1
p+1光滑
William’s p+1 分解算法。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 def mlucas (v, a, n ): """ Helper function for williams_pp1(). Multiplies along a Lucas sequence modulo n. """ v1, v2 = v, (v**2 - 2 ) % n for bit in bin (a)[3 :]: v1, v2 = ((v1**2 - 2 ) % n, (v1*v2 - v) % n) if bit == "0" else ((v1*v2 - v) % n, (v2**2 - 2 ) % n) return v1 for v in count(1 ): for p in primegen(): e = ilog(isqrt(n), p) if e == 0 : break for _ in xrange(e): v = mlucas(v, p, n) g = gcd(v-2 , n) if 1 < g < n: return g if g == n: break
Coppersmith定理指出在一个 e 阶的 mod(n) 多项式 f(x) 中，如果有一个根小于 n1e，就可以运用一个 O(logn) 的算法求出这些根。
格密码
线性独立空间上有集合 v_1,\cdots,v_n \in \mathbb{R}^n，格（Lattices）就是这些向量的线性组合，用公式表示为：
L={a_1v_1+a_2v_2+\cdots+a_nv_n \mid a_1,a_2,\cdots,a_n \in \mathbb{Z}}。
格 L 的维数等于格中向量的个数。
假定 v_1,v_2,\cdots,v_n 是格 L 的基，w_1,w_2,\cdots,w_n \in L，则必然存在整系数 a_{ij} 使得：
\begin{cases} w_1=a_{11}v_1+a_{12}v_2+\cdots+a_{1n}v_n \ w_2=a_{21}v_1+a_{22}v_2+\cdots+a_{2n}v_n \ \vdots \ w_n=a_{n1}v_1+a_{n2}v_2+\cdots+a_{nn}v_n \end{cases}
这样，格的问题就是矩阵运算了。
因为，由引理2可得
也是p的一个完全剩余系。
没有正整数解。
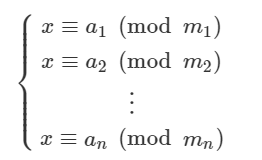
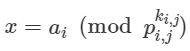,其中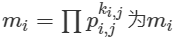
为$m_i$的分解式
