普及数学知识

模运算

同余:两个整数a,b弱它们除以正整数n所得的余数相等,则称a和b对于模n同余,

记作a≡b(mod n)

读作a同余b与模n,或a和b关于模n同余.

模逆元

参考倒数xy=1的定义,对于整数a和b,若ab=1(mod n).

则成a和b关于模n互为模倒数,也叫模逆元,还可以记作b≡1 / a(mod n)

也就有c/a mod n = (c*1/a) mod n = ((c mod n) * 1/a mod n) mod n =
((c mod n) * (b mod n)) mod n = (c * b) mod n

如:20/3mod7=((20mod7)⋅(1/3mod7))mod7=(6×5)mod7=2

加密算法

1
c =m^e(mod N)

解密算法

1
m = c^d (mod N)

n的欧拉函数就等于

phi = (p - 1) * (q - 1) * (r - 1)的原因：

根据欧拉函数，如果存在n可以分解成两个互质的整数之积，即

n = p1 * q1

则存在这样的关系：

phi(n) = phi(p1q1) = phi(p1) * phi(q1) = （p1 - 1） (q1 - 1)

举个例子：

n = 56，则phi(56) = phi(8 * 7) = phi(8) * phi(7) = 4 * 6 =24

d=gmpy2.invert(e,phi)

gmpy2.invert(a, b)函数用于计算a在模b下的乘法逆元，即找到一个数x，使得 (a * x) % b == 1。其中a和b是gmpy2中的mpz类型，返回值也是一个mpz类型。

1
2
3
(e*d)%phi==1          e*d=phi
e^dmod φ(n) = 1

费马小定理

如果 p 是一个质数，而整数 a 不是 p 的倍数，则

a p−1 ≡ 1 (mod p)

可得

a * a p−2 ≡ 1 (mod p)

所以 a 的逆元即为 a p-2 (mod p)

之后利用快速幂求解

欧拉函数

小于n且与n互素的个数就是欧拉函数,记为φ(n)

欧拉函数具有以下性质:

  • 如果n为素数,则小于所有n的正整数都与n互素,那么φ(n)=n-1

  • 如果gcd(p,q)=1,那么φ(p*q) = φ§*φ(q)

  • 如果整数n因数分解为n=p1,p2,…,pn,p1,p2,…,pn为互不相同的素数，那么Φ(n)=n(1 - 1/p1)(1 - 1/p2)…(1 - 1/pn)

欧拉定理

对于任何互质的正整数a和n,有aΦ(n) = 1(mod n)

扩展欧几里得

逆元的含义决定了ax ≡ 1(mod b)等价于ax = kb+1

1
2
3
4
5
6
7
8
void exgcd(int a, int b, int& x, int& y) {
  if (b == 0) {
    x = 1, y = 0;
    return;
  }
  exgcd(b, a % b, y, x);
  y -= a / b * x;
}

单向函数

定义:一个可逆函数f:A->B,若它满足:

  • 对所有x∈A，易于计算f(x)
  • 对”几乎所有x∈A”由f(x)求x极为困难，以至于实际上不可能做到
    则称f为一单向函数。

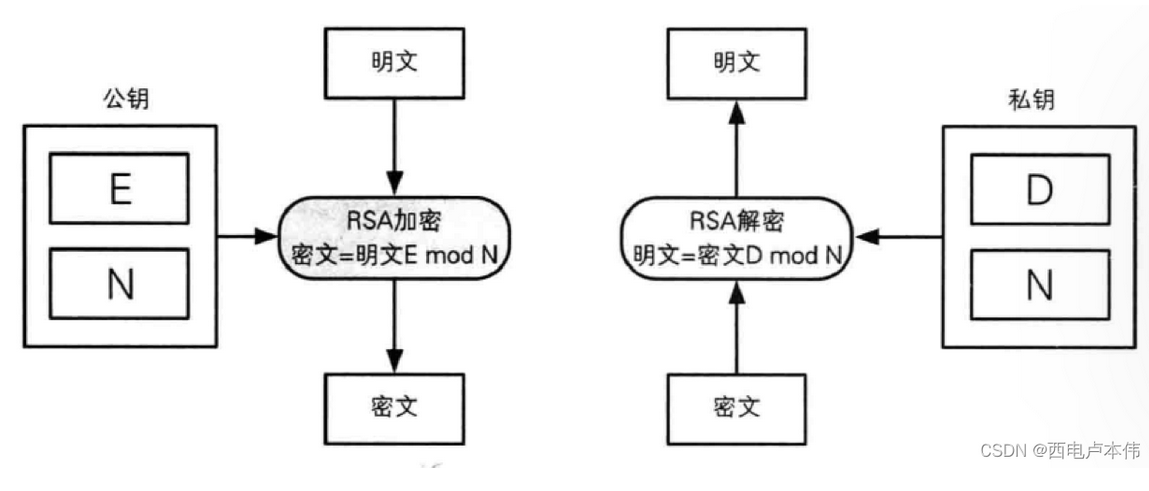
RSA 算法解释(简)

https://www.wanan.red/623b8b34.html#RSA算法解释

加密算法

c =m^e(mod N)

其中c作为密文 m作为明文

也就是说在e与N作为RSA加密算法的公钥,也就是(e,N)公钥可公开

解密算法

m = c^d(mod N)

即RSA的明文就是代表密文字符c的d次方对N求余的结果 那么这里的(d,N)便作为私钥

既然公钥与私钥之中都存在有 N,那么 N 不就是代表 公开的吗 那么其中主要保存的其实就是 e (encode 编码) 与 d (decode 解码)

image-20220906162155058

生成密钥对

由上面可知,我们生成密钥对的时候需要三个参数n e d,接下来我们看看它是如何生成的.

求n

首先需要准备两个极大的指数P Q

P*Q=N

求φ

φ=(P-1)*(Q-1)

求e

e 的求解基于上述的 φ 值 首先需要明确 e 的取值范围 1 <e < φ , 并且 gcd (φ , e) = 1 (即 φ 与 e 的最大公约数为 1, 即两者互质) 之所以需要添加 1 这个值，是为了保证存在解密时需要使用的参数 D

求d

首先需要明确d的取值范围1<d<φ,并且gcd(φ,d)=1

e*d(mod φ)=1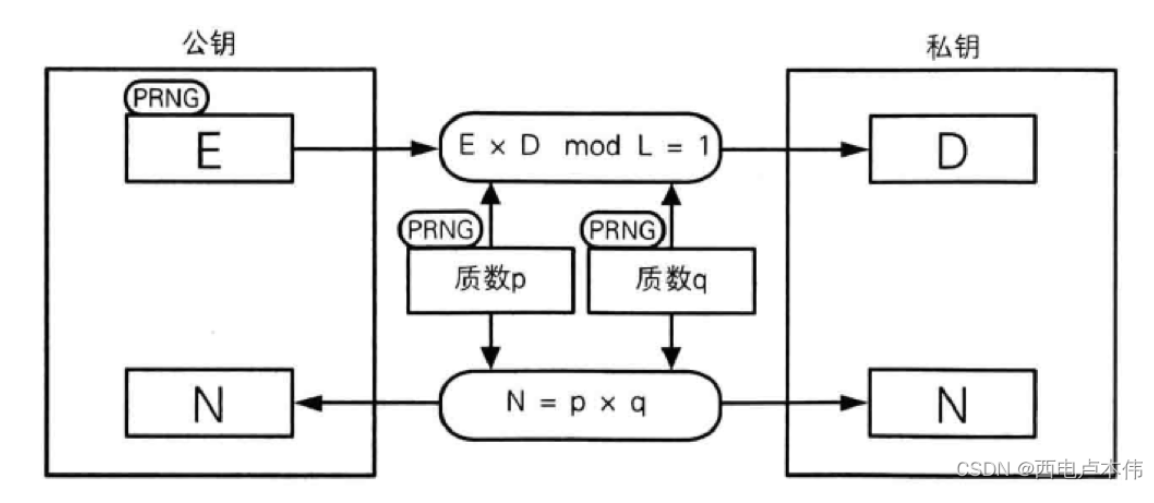image-20220906162206289

举例

(正常来说,需要准备两个极大的指数P Q,但是这样容易懂一些)

求N

首先随便找两个素数，比如3、11(这边自己实验就取小数展示)

p = 3
q = 11

得到 N

N = 3*11 = 33

求φ

φ = 2*10= 20

求e

gcd(φ,e)=1

满足条件的有很多，3，7，11，13，17，19… 这边我们选择3来作为 e。
至此，e = 3 ，N = 33，这就是公钥

求d

e*d mod φ=1

容易得 d = 7
至此，d = 7 ，N = 33，这就是私钥

加密

要加密的明文必须是小于 N 的数，也就是小于33的数，这边就随便取一个5吧

c=me mod N = 53 mod 33 = 26

解密

m=cd mod N = 267 mod 33 = 5

libnum库的应用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
import libnum
#生成素数
p=libnum.generate_prime(1024)
q=libnum.generate_prime(1024)
#字节、数字转换
flag="flag"
a=libnum.s2n(flag)
b=libnum.n2s(a)
print(a)
print(b)
#二进制、数字转换
flag="flag"
a=libnum.s2b(flag)
b=libnum.b2s(a)
print(a)
print(b)
#求逆元
libnum.invmod(e,phi)
#求最大公约数
libnum.gcd(a,b)
#求最小公倍数
libnum.lcm(a,b)
#开方
libnum.nroot(a,b)
#中国剩余定理
libnum.solve_crt()
#扩展欧几里得算法
libnum.xgcd(a,b)

import gmpy2
#判断是否为素数
gmpy2.is_prime()
#判断是否为完全平方数
gmpy2.is_square()
#生成下一个素数
gmpy2.next_prime()
#求逆元
gmpy2.invert()
#开方
gmpy2.iroot()
#返回数字二进制的长度
gmpy2.bit_length()
#扩展欧几里得算法
gmpy2.gcdext()
#
import sympy
#返回上一个素数
sympy.prevprime()